在《设定集》中提到,三维空间五种正多面体代表四大元素加以太,而扩展到四维空间,六种正多胞体代表四大元素加正负能量,而「以太」因为长期无法证实而被放弃。那么就要考虑本位面哲学史和物理学史当中「以太」的待遇浮沉,设想万一于「卡壳世界」再次被提起的时候,数学界如何修改模型。
由于政治无处不在,革命进步势力与反动落后势力之间的拉锯战是长期的艰巨的复杂的残酷的,而进步学者「希帕索斯会」与反动学者「走毕达哥拉斯路线的当权派」之间的斗争也是同样长期的艰巨的复杂的残酷的。所以仍然需要设定两个针锋相对的数学模型。
在勾结反动当局的反动学者走毕派那边,决定安排为「反攻倒算」,企图恢复三维空间几何理论的统治地位。而三维空间的「正多面体」,除了五种众所周知的「正『凸』多面体」之外,还有四种「正『凹』多面体」,或曰「星形正多面体」:
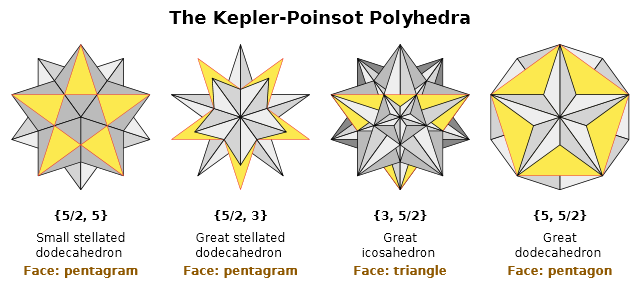
其中左边两个「小星形十二面体」「大星形十二面体」是开普勒「重新」发现的或者说在数学上严格「定义」的。「14世纪Paolo Uccello的画作出现了小星形十二面体。15世纪Wenzel Jamnitzer发现小星形十二面体和大星形十二面体」。而右边两个「大二十面体」「大十二面体」则是路易・庞索(Louis Poinsot)发现的。
开普勒于1619年「定义」了「星形化」操作,就是将凸图形各边内折但不增加新的「顶点」,也就是说折边的「延长线」会与对面折边重合。各位读者用正五边形和正五角星类比就可以了也,同样是五条线段画出来的图形,却凹凸有别。
而「哈罗德・斯科特・麦克唐纳・考克斯特」(Harold Scott MacDonald “Donald” Coxeter,1907年2月9日-2003年3月31日)则证明了若正多面体$\{p, q\}$的Petrie多边形(指两个连续边都属于多面体的一个面,但三边不属多面体的面的不共面多边形)有$h$条边,则有
$$cos^2\frac{\pi}{p}+cos^2\frac{\pi}{q}=cos^2\frac{\pi}{h}$$当 $p, q, h$ 均为正整数时,有5组解,对应众所周知的五个正凸多面体。而$p, q, h$为正有理数时,多了4组解,分别对应四个星形正多面体。其中记号$\{p, q\}$是「施莱夫利(Schläfli)符号」,在正多面体的场合,$p$代表每个面的边数,而$q$代表顶点图的边数。
路德维希・施莱夫利(Ludwig Schläfli,1814年1月15日-1895年3月20日)是一个发展高维空间概念的重要人物,手稿在死后的1901年才全部出版。很少人记得他,虽然多维概念后来已经成为包括但不限于「当代主流物理价值观」的关键。
所以,准备在设定中安排施莱夫利作为希帕索斯会成员,默默耕耘但成果被走毕派剽窃,由于「卡壳世界」几何学研究更流行更深入更发达,所以这位的出场时间会更早。
而这四种星形正多面体,准备用来对应本位面「四大基本力」的「卡壳世界」中被走毕派提出的四大「以太」。就是说,「以太」复活之后被官方学术界一分为四,用来代表可类比「场」的概念。
率先被发现的两种开普勒多面体当然对应引力和电磁力。在注释中提到过,我在构思「卡壳世界」从托勒密体系到开普勒体系的转变的时候,想找到一个数学上顺理成章的过程。在最初上传正文之前都没想好。而随着注释以及开始恶补数学,逐步有了一点点思路,初步决定用开普勒多面体作为过渡,是构思的一个成果,但还算不上突破。
注意「开普勒立体」是几何形状的命名,如同柏拉图立体阿基米德立体卡塔兰立体一样,本身不代表冠名者的政治和意识形态倾向。按照设定中时间线,走毕派拿来主义的时候,开普勒已经过世。
而晚了许久才被发现的两种「庞索立体」,当然就被拿来对应强力弱力喽。并且这「路易・庞索」是法国人,时间也凑巧是「法帝野心狼」兲命昭昭时期,但是本人知名度不高尽量不安排出场。留给读者脑补,或是走毕派推出来挂名,或是完全与政治无关。
这是反攻倒算的复古派观点,注意学术上未必没有道理。为了激化矛盾制造冲突增加剧情跌宕起伏程度,我尽量选择各种立场之间的正交关系以尽可能扩大组合可能性。这与本位面当代「作者编剧导演」只会「豪门恩怨伦理剧」「校园欺凌青春剧」「争风吃醋肥皂剧」等烂大街套路翻来覆去循环播放让观众看到审美疲劳的拙劣伎俩形成鲜明对比。
而「与时俱进派」观点,还是在「近世元素魔法」的四维空间当中发展。四维空间的正多胞体也一样,除了「凸」的六种之外,还有「凹」的十种「星形正多胞体」呢。这么看来,「四维以太」复杂程度比三维要多,正好可以结合恶补进度,尽量往四维空间微分结构「变化无穷」方向进展。